4.6. Combinatorics#
“Counting is the religion of this generation… Anybody can count…” – Gertrude Stein
Interactive Quizzes
This page has several different sets of quizzes that are meant to be taken as indicated in the text of the book. \(~~~~ ~~~~ ~~~~\)
Combinatorics Question 1
Combinatorics Question Set 2
Combinatorics Question Set 3
Additional Review Questions
Terminology Review
Use the flashcards below to help you review the terminology introduced in this chapter.
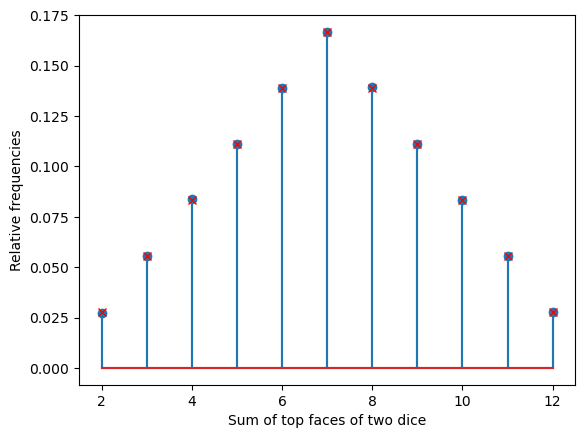
Code for calculating probabilities and plotting for Example 4.9: (A) Monopoly Dice
The following code finds the probabilities for the values that arise from rolling two dice and adding the values. For instance, this is the method used by each player to determine how many spaces to move in the classic game Monopoly. The probabilities are found in two ways, corresponding to how they are found in this portion of Foundations of Data Science with Python:
They are found by enumerating all outcomes of the combined experiment and then counting the number of ways each sum can occur.
The probabilities are estimated by the results of a simulation of 1 million rolls of the pairs of dice.
Note that these probabilities can also be found using combinatorics; an example is given in Example 4.12 of the book.
# Calculate probs via combinatorics:
import itertools
S0 = range(1, 7)
S1 = range(1, 7)
S = itertools.product(S0, S1)
Slist = list(itertools.product(S0, S1))
counts = [0] * 13
for s in Slist:
counts[sum(s)] += 1
probs = [0] * 13
for c in range(2, 13):
probs[c] = counts[c] / len(Slist)
import numpy as np
import numpy.random as npr
import matplotlib.pyplot as plt
die1 = npr.randint(1, 7, size=1_000_000)
die2 = npr.randint(1, 7, size=1_000_000)
dice = die1 + die2
vals, mycounts = np.unique(dice, return_counts=True)
rel_freqs = mycounts / len(dice)
plt.stem(vals, rel_freqs)
plt.stem(range(2, 13), probs[2:13], markerfmt='rx')
plt.xlabel('Sum of top faces of two dice')
plt.ylabel('Relative frequencies');